二阶常系数齐次线性微分方程通解
本文核心词:微分方程,线性无关,通解
下面的微分方程,为二阶常系数齐次线性微分方程。
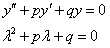
微分方程与特征方程
当特征方程的解为两个不同的实根时,微分方程的通解为:

若为两个相同重根:
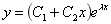
若为共轭虚根:
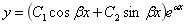
但这些都是怎么来的呢,为何要用特征方程来辅助研究呢?为了解决这一问题,我去图书馆查阅了一些电子资料才得知。
对于齐次线性微分方程,形如下面:

线性微分方程的解有无数个,但是它解的结构有点类似线性方程组,在无数个解当中有一组线性无关的解,找出他们就可以表示其他所有解。可是,怎么判断方程有几个线性无关的特解呢?这时候就需要特征方程来辅助了。

特征方程中P(x)可看作一个常数
这种微分方程的解具有什么样的结构,取决于它的系数函数P(x)和阶数。我们设计一个一元 n次方程,未知数最高次数对应微分方程的最高阶数,把微分方程的系数函数作为一元n次方程未知数的系数,这样,一元n次方程有几个解就能说明微分方程有几个线性无关特解。
根据代数基本定理,复系数一元n(n=1)次多项式在复数域至少有一个根,重根按重复次数计算(只有一个根说明有n个相同重根)。这就注定了特征方程一定有n个解,对应的n阶微分方程就有必n个线性无关特解。
什么叫线性无关呢?按照我个人的理解,对于两个量来说,它们两个相除后,得数不是常数(成比例)就无关,对于多个量来说就是不能相互表示。
打一个不太恰当的比方,七个葫芦娃个个本事都不一样,谁也无法替代谁,就算前六个葫芦娃联手也无法替代老七宝葫芦的重要作用。但是他们合体成葫芦小金刚就不一样了,如果把小金刚算作第八个葫芦娃,那么他们八个就线性相关了,因为小金刚会的技能无非就是前七个技能的组合,并没有多出来新技能,前七个葫芦娃就算不合体,相互配合打团战,也是可以打出小金刚一个人的作战效果的。总之,用数学化语言讲,葫芦小金刚是七个葫芦娃的线性表示(单从技能组合上来看)。
在一组函数中,如果每一个函数都无法被其他函数表示,那么这一组就线性无关。
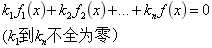
线性无关
那么对于二阶常系数齐次线性微分方程就更简单了。

我们只需要找到两个无关的特解就可以线性表示所有的解。我观察后突然发现,二阶导、一阶导和原函数之间就差了个常数p和q,那得有一个函数求导后之和原来相差一个常数。学过的初等函数中只有自然函数e做底数的指数函数和常数函数。
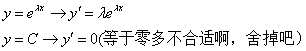
我们把候选函数代进方程里:
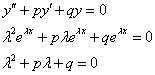
结果就是特征方程
所以λ取什么值完全要看特征方程的眼色,如果是两个不同实根,那两个无关特解就可以这样设:

如果是两个相同重根,这样设:
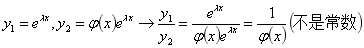
将y2代入微分方程后:

若是两个共轭虚根:
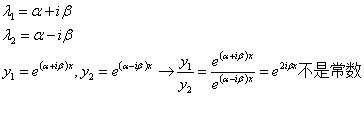
根据欧拉公式:
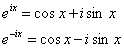
可以将它变换:

线性微分方程的解的结构和线性方程组类似,可进行类比。
以前我学习微分方程都是直接背公式的,也不知道它是怎么来的,心里一直因为这个阴云不散,不管是做相关的题目还是解决力学上的微分方程,总是提笔忘式,我下定决心要弄清楚。我觉得,对一个知识一定要立体的,多方位的学习才能牢牢掌握。如果不是去探究微分方程通解的数学原理我可能都不知道欧拉公式能这么用,并且我也在探究的过程中享受到了“朝闻道夕死可矣”的快乐。
下笔要想有神,必须要对自己的知识清清楚楚。

好啦,以上就是二阶常系数齐次线性微分方程通解全部内容,都看到这里了还不收藏一下??搜索(微分方程,线性无关,通解)还能找到更多精彩内容。