易混基础概念
标量:单独一个数
向量:一行/列数
矩阵:二维数组
张量:一般指多维 0 维张量是标量,1 维张量是向量,2 维张量是矩阵
转置:沿主对角线折叠
在 Numpy 中定义矩阵的方法,以及进行转置的方法:
importnumpyasnpa=np.array [[1,2,3],[4,5,6]]a=a.reshape 3,2print a[[12][34][56]]复制代码基本算数关系
与高等数学中矩阵相乘内容一致:
a=np.array [[1,2],[3,4]]b=np.array [[5,6],[7,8]]print a*bprint a.dot bprint np.dot a,bprint np.linalg.inv a#星 *[[512][2132]]#点乘[[1922][4350]]#点乘[[1922][4350]]#逆运算[[-2.1.][1.5-0.5]]复制代码范数
范数是一个函数,用于衡量长度大小的一个函数。数学上,范数包括向量范数和矩阵范数。
向量范数
我们先讨论向量的范数。向量是有方向有大小的,这个大小就用范数来表示。
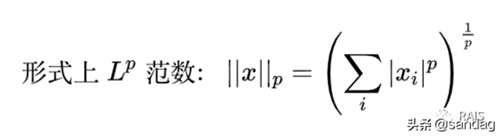
严格意义上来说,范数是满足下列性质的任意函数:
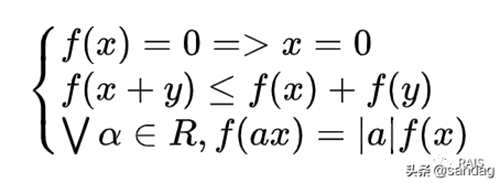
当 p=2 时,范数 ,可简化写成称为欧几里得范数,可以计算距离。但是我们看到这里有一个开方运算,因此为了去掉这个开方,我们有可能求的是范数的平方,即范数,这就会减少一次开放运算,在后面提到的损失函数中,范数和平方范数都提供了相同的优化目标,因此平方范数更常用,计算起来也更简单,可以通过计算,这速度就很快了。
当 p=1 时,范数 是向量各元素绝对值之和,在机器学习领域,对于区分 0 和非 0 来说,范数比范数更好用。
当 p=0 时,范数实际上不是一个范数,大多数提到范数的地方都会强调说这不是一个真正意义上的范数,用来表示这个向量中有多少个非 0 元素,但是实际上它是非常有用的,在机器学习中的正则化和稀疏编码中有应用。在一个例子中是这么说的:判断用户名和密码是否正确,用户名和密码是两个向量,时,则登录成功,时,用户名和密码有一个错误,时,用户名和密码都错误。我们知道有这么回事,在日后看到相关内容时知道就好了。
当 p 为无穷大时,范数也被称为无穷范数、最大范数。表示向量中元素绝对值中最大的。
矩阵范数
对于矩阵范数,我们只聊一聊 Frobenius 范数,简单点说就是矩阵中所有元素的平方和再开方,还有其他的定义方法,如下,其中表示的共轭转置,tr为迹;表示的奇异值:
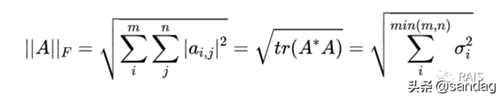
奇异值分解
我们熟悉特征分解矩阵中:,奇异分解与之类似:,其中矩阵的行和列的值为、正交矩阵、对角矩阵、正交矩阵,矩阵对角线上的元素称为的奇异值,其中非零奇异值是或的特征值的平方根;称为的左奇异向量,是的特征向量;称为的右奇异向量,是的特征向量。因为奇异矩阵无法求逆,而求逆又是研究矩阵的非常好的方法,因此考虑退而求其次的方法,求伪逆,这是最接近矩阵求逆的,把矩阵化为最舒服的形式去研究其他的性质,伪逆把矩阵化为主对角线上有秩那么多的非零元素,矩阵中其他的元素都是零,这也是统计学中常用的方法,在机器学习中耶非常好用。
定义
对角矩阵:只有主对角线含有非零元素;
单位向量:具有单位范数的向量,;
向量正交:如果两个向量都非零,则夹角 90 度;
标准正交:相互正交、范数为 1;
正交矩阵:行向量和列向量分别标准正交;
特征分解:将矩阵分解为特征向量和特征值;
特征值和特征向量:中的和;
正定、半正定、负定:特征值都正、非负、都负。
总结
线性代数的一大特点是“一大串”,统一的知识体系,相互之间紧密联系,非常漂亮,在深度学习中有重要的应用,还是应该要学好。
关于 矩阵的范数怎么求 深度学习中的线性代数今天就说到这里,喜欢记得收藏一下。搜索()还能找到更多相关文章。